Most people enjoy playing Jenga. Picture yourself in a room filled with an infinite number of identical Jenga blocks, disregarding their depth.

Jenga blocks

You become curious about the length-to-width ratio of a Jenga block but lack any measuring tools. Nevertheless, you devise a method to determine this ratio by arranging the blocks vertically and horizontally.

A solution finding length-to-width ratio

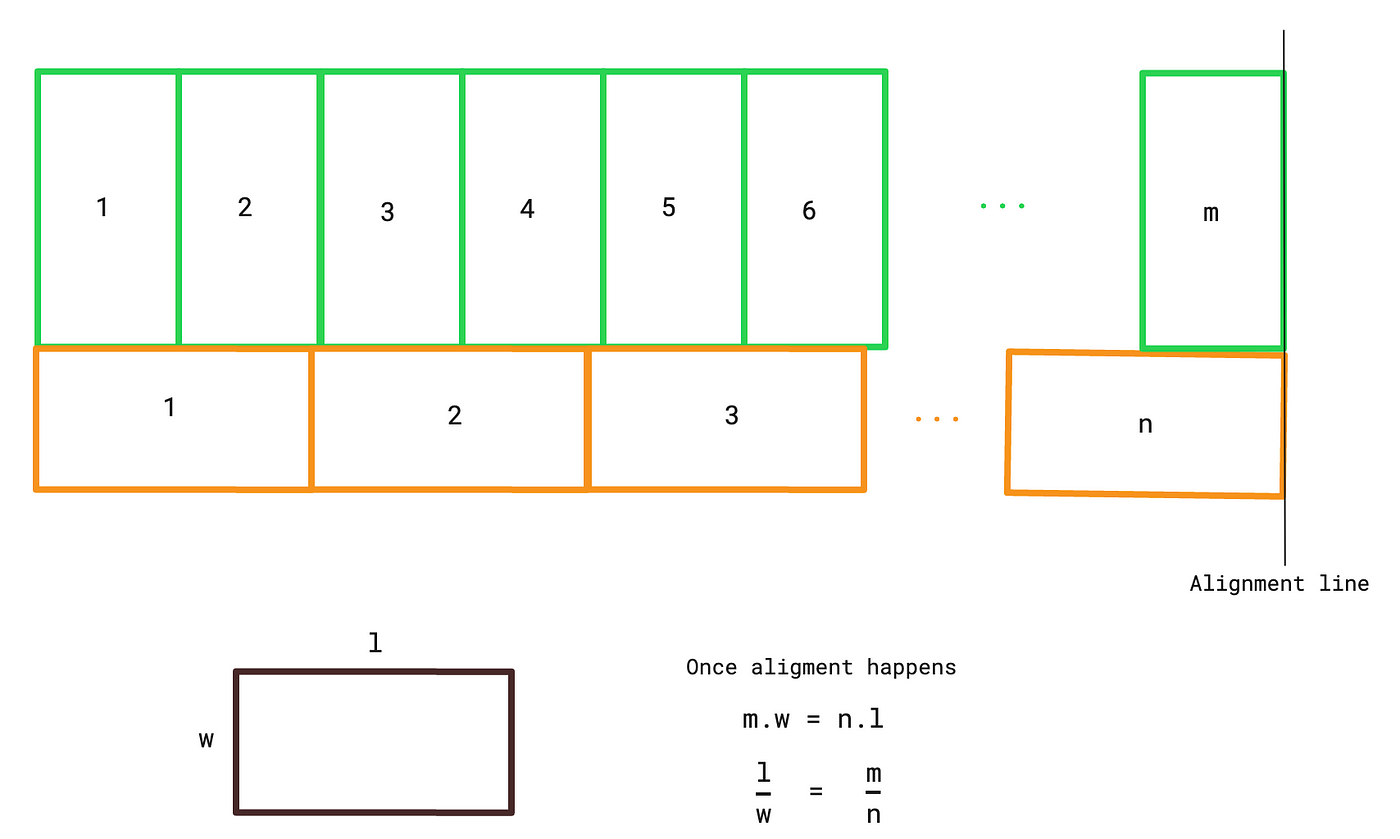
To find the length-to-width ratio, you count the number of vertical and horizontal blocks used once they align (vertical blocks / horizontal blocks).

\[\frac{\textrm{number of vertical blocks}}{\textrm{number of horizontal blocks}} = \frac{l}{w}\]

However, you observe that these Jenga blocks never truly align, only coming closer to alignment. You wonder what is unique about their length-to-width ratio.

The answer is that the ratio is an irrational number.

To represent an irrational number, you would need an infinite number of blocks, as it is impossible to represent such a number within a finite domain. The length-to-width ratio is a real value in your hand, yet it cannot be represented in a finite world. Irrational numbers like $\sqrt{2}$ and $\pi$ are merely symbols that indicate their existence.